When the array or list are already sorted,then we are lucky ,because there is no need to scan all the element of array or list. here we will take the advantage of already ordered list, and applied some condition to break the further traversing.
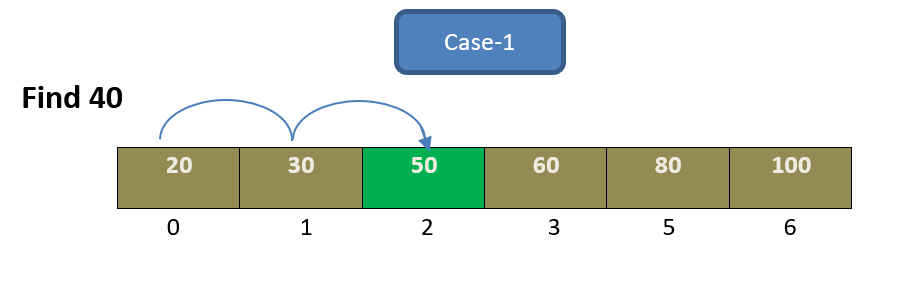
Here if we apply following code algorithm on the above sorted array,here 50 is greater than 40(target value), after 50 , there is no need to go further because after 50 all the element will be greater than 50,but our target is 40.
So here we can break the iteration.that is the advantage of sorted array.
#include <stdio.h>
int OrderedSearching(int List[],int Target,int ListSize)
{
for(int i=0;i<ListSize;i++)
{
if(List[i]==Target)
return i;
else if(List[i]>Target)
{
return -1; // When Target is not available in the List.
}
}
}
int main()
{
int A[]={20,30,50,60,80,100};
int ListSize = sizeof(A) / sizeof(A[0]);
int Target=40;
int indexVal=OrderedSearching(A,Target,ListSize);
if(indexVal==-1)
{
printf("Element is not in the List,So dont go further Iteration..");
}
else
{
printf("Index of Target is %d :",indexVal);
}
return 0;
}But anyway above code is not much good for sorted array, we can improve our algorithm to reduce the complexities.For Sorted Array generally we use Binary Search which will be discussed in next chapter.
Time and Space Complexity
Time Complexity will be similar to the Unordered Linear Search,
for Worst Case : Time Complexity will be O(n).
for best Case : Time Complexity will be O(1).
for average Case : Time Complexity will be O(n/2)=O(n).
and Space Complexity will be O(1)