Binary Search

In Binary Search algorithm,During the search an element we reduce the array size by half in every search iteration.

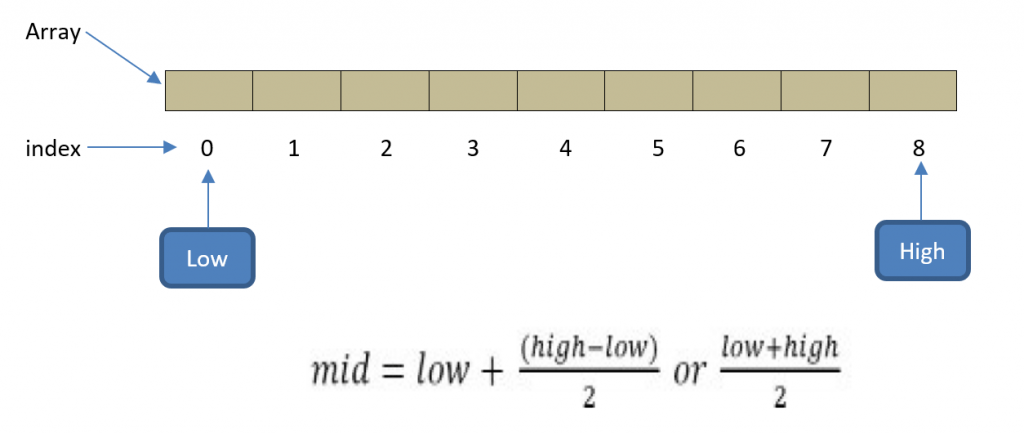
We use the three parameter (Low,mid,High). Low indicates the first index of array ,High indicates the Last index of array and for finding mid, we use above formula.
When mid value is in float like 3.5 or 3,4 etc,then we can apply floor or ceil Concepts on mid.
Example : floor(3.5)=3 , floor(3.8)=3,ceil(2.1)=3,ceil(3.5)=4 etc.

After getting Low,mid and High then we will apply following conditions :
Cond1: If Array[mid] ==Target then we got the Target Element.
Cond2: if Array[mid] > Target then Low=Low and High=(mid-1).
Cond3: if Array[mid] < Target then Low=(mid+1) and High=High.
These condition will be applied until we get the Target.

Explanation of Binary Search By Example

See the Below Example :

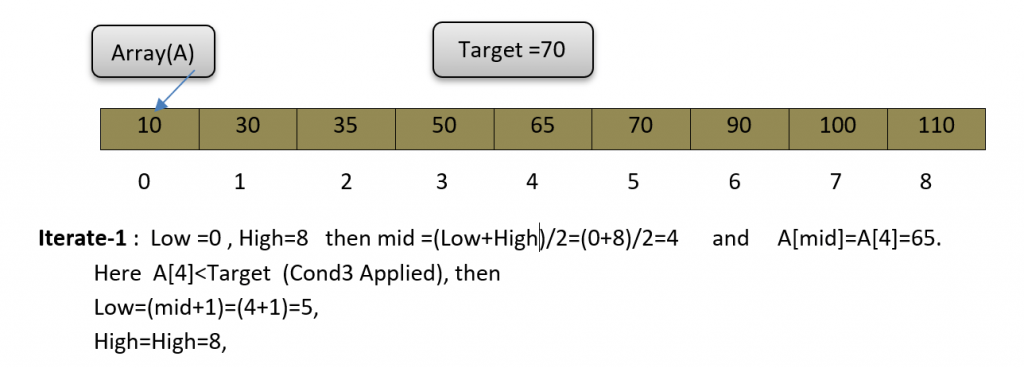
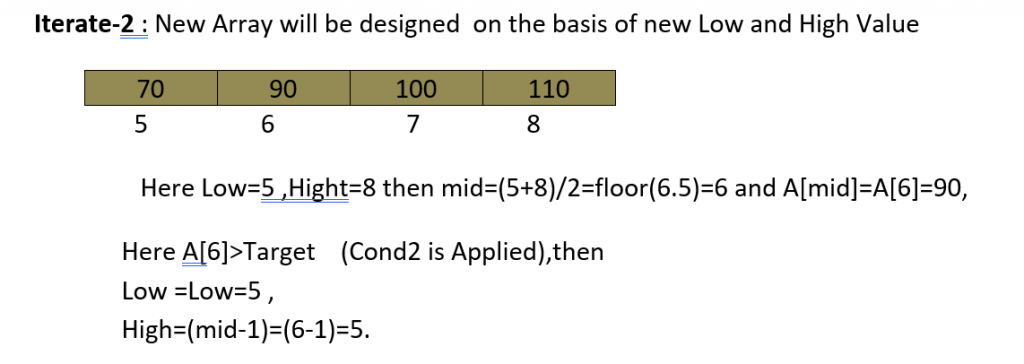
Code For Binary Search

We can implement Binary Search by 2 Types :
1- By Iteration Method
2- By Recursive Method
We will discuss both implementation Type.

1- By Iteration Method

In this method, Binary Search is implemented on basis of the Iterative Paradigm.

    #include <stdio.h>
    int BinarySearchIterativeMethod(int List[],int Target,int Low,int High)
    {
        int mid;
        while(Low<=High)
        {
          mid=(Low+High)/2;
          if(List[mid]==Target)       //Cond1 is here
          {
            return mid;
          }
          else if(List[mid]>Target)   //Cond2 is here
          {
              High=mid-1;
          }
          else                        //Cond3 is here
          { 
              Low=mid+1;
          }
        }
        return -1;        //When Target is not available in the List.
    }
    int main()
    {
        int A[]={10,30,35,50,65,70,90,100,110};
        int ListSize = sizeof(A) / sizeof(A[0]);
        int Low=0,High=ListSize-1;
        int Target=10;
        int indexVal=BinarySearchIterativeMethod(A,Target,Low,High);
        if(indexVal==-1)
        {
            printf("Element is not in the List");
        }
        else
        {
            printf("Index of Target is %d :",indexVal);
        }
        return 0;
    }

2- By Recursive Method

In this method ,we use recursive function to implement Binary Search.But Anyway Recursive implementation is not a good approach for any algorithmic implementation,we should avoid the recursion in our implementation.

    #include <stdio.h>
    int BinarySearchRecursiveMethod(int List[],int Target,int Low,int High)
    {
        int mid;
        while(Low<=High)
        {
          mid=(Low+High)/2;
          if(List[mid]==Target)       //Cond1 is here
          {
            return mid;
          }
          else if(List[mid]>Target)   //Cond2 is here
          {
              return BinarySearchRecursiveMethod(List,Target,Low,mid-1);
          }
          else                        //Cond3 is here
          { 
              return BinarySearchRecursiveMethod(List,Target,mid+1,High);
          }
        }
        return -1;        //When Target is not available in the List.
    }
    int main()
    {
        int A[]={10,30,35,50,65,70,90,100,110};
        int ListSize = sizeof(A) / sizeof(A[0]);
        int Low=0,High=ListSize-1;
        int Target=10000;
        int indexVal=BinarySearchRecursiveMethod(A,Target,Low,High);
        if(indexVal==-1)
        {
            printf("Element is not in the List");
        }
        else
        {
            printf("Index of Target is %d :",indexVal);
        }
        return 0;
    }

Time & Space Complexity

We know that ,In binary search we reduce the size of list/array by half for every iteration.So Recurrence Relation for Binary Search will be :
T(n) =T(n/2) + Θ(1)
Apply Master Theorem and we will get Time Complexity :
T(n) =O(Logn) and Space Complexity will be O(1).
Space Complexity will be O(1) only for Iterative Implementation of Binary Search.For Recursive Implementation of Binary Search need a lot of memory,So Space complexity will be different.

Note

Following Points must know about the Binary Search :

Binary Search is applicable only on sorted data, means array or list must be Ordered or Sorted.
Binary Search can be use when Data Structure must support the Random searching.