- BFS is a type graph traversal algorithm ,means if we want to visit on every node/vertices through their connected edges.
- BFS is the complement of Depth First Search(DFS).
- BFS use a Queue Data Structure.
- BFS explore the all the vertices level by level ,means it visit level-1 to next level and till last level of Graph.
Procedure
Initialize an Graph G(V,E).and create an empty Queue.Start from any Vertex(Node). Now Apply Below rules :
Rule-1 : Check selected Node is already visited or not. if node id already visited then directly go to the Rule-3.
Rule-2 : Marks selected as visited Node, and insert their neighbor into Queue.
Queue must be unique ,means if a node is already inserted then there is no need to insert again.
Rule-3 : Pick one Node element from the Queue by applying delete operation on Queue.
Rule-4 : Repeat Rule-1,Rule-2 and Rule-3 until Queue is empty.
Explanation of BFS by Example
Below is the Graph G(V,E). we will Start from Node A. and initialized one queue Q which is empty :
- Green Color : Visited Node
- Blue Color : Neighbor of Selected Node from the Queue
- Yellow Color : Selected Node from the Queue.
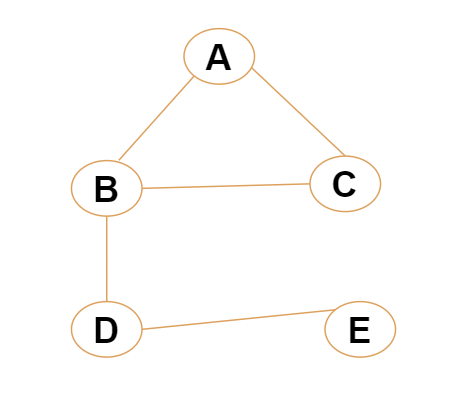

- Queue is Q={}.
- Here we have selected Node A. and marked as Yellow.
- Neighbor of A is B and C.
- insert B and C into Queue Q.So Q= {B,C}
- Marks A as Visited means color it by Green.

- Queue is Q={B,C}.
- Delete one element from Q,that will be selected Node B.
- Here we have selected Node B. and marked as Yellow.
- Neighbor of B is A,D and C,
But A is visited,No need to insert, C is already available in Queue Q ,then no need to insert again. - insert only D into Queue Q.So Q= {C,D}.
- Marks B as Visited means color it by Green.

- Queue is Q={C,D}.
- Delete one element from Q,that will be selected Node C.
- Here we have selected Node C. and marked as Yellow.
- Neighbor of C is A,B .But A and B are already visited.So No need to insert.
- Q= {D}.
- Marks C as Visited means color it by Green.

- Queue is Q={D}.
- Delete one element from Q,that will be selected Node D.
- Here we have selected Node D. and marked as Yellow.
- Neighbor of D is B and E ,But B is already visited.So No need to insert B.
- Insert E into Queue Q= {E}.
- Marks D as Visited means color it by Green.

- Queue is Q={E}.
- Delete one element from Q,that will be selected Node E.
- Here we have selected Node E. and marked as Yellow.
- Neighbor of E is D ,But D is already visited.So No need to insert D.
- Q= {}.
- Marks E as Visited means color it by Green.

- Queue is Q={}.
- Now Queue is Empty , we will close the Process.
- When Queue is empty means all nodes or vertices are visited.
Animation of BFS

Code Implementation of BFS
#include<iostream>
#include <list>
using namespace std;
//class CreateGraph is used to Create a graph by
//adjacency List.
class CreateGraph
{
int V; // Number of vertices
// Pointer to an List containing adjacency lists
list<int> *adj;
public:
CreateGraph(int V); // Constructor
// Addition of an edge to graph
void EdgeAddition(int v, int w);
// BFS traversal function from a given source s
void BFSAlgorithm(int startNode);
};
CreateGraph::CreateGraph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void CreateGraph::EdgeAddition(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void CreateGraph::BFSAlgorithm(int startNode)
{
// Mark all the vertices as unvisited.
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
// queue for BFS
list<int> queue;
// Mark the current node as visited and enqueue it
visited[startNode] = true;
queue.push_back(startNode);
// adjVer will be used to get all adjacent vertices of a vertex
list<int>::iterator adjVer;
while(!queue.empty())
{
// Dequeue(Delete) a vertex from queue.
startNode = queue.front();
cout << startNode << " ";
queue.pop_front();
// Get all adjacent vertices of the dequeued
// vertex s. If a adjacent has not been visited,
// then mark it visited and enqueue it
for (adjVer = adj[startNode].begin(); adjVer != adj[startNode].end(); ++adjVer)
{
if (!visited[*adjVer])
{
visited[*adjVer] = true;
queue.push_back(*adjVer);
}
}
}
}
//Main function
int main()
{
// Create a graph by Graph
CreateGraph NumberOfNode(5); //Number of Node is 4
NumberOfNode.EdgeAddition(0, 1); //Node-0 is connected to Node-1
NumberOfNode.EdgeAddition(0, 2); //Node-0 is connected to Node-2
NumberOfNode.EdgeAddition(1, 2); //Node-1 is connected to Node-2
NumberOfNode.EdgeAddition(1, 3); //Node-1 is connected to Node-3
NumberOfNode.EdgeAddition(2, 0); //Node-2 is connected to Node-0
NumberOfNode.EdgeAddition(2, 1); //Node-2 is connected to Node-1
NumberOfNode.EdgeAddition(3, 1); //Node-3 is connected to Node-1
NumberOfNode.EdgeAddition(3, 4); //Node-3 is connected to Node-4
NumberOfNode.EdgeAddition(4, 3); //Node-4 is connected to Node-3
cout << "Sequence of traversal of BFS : "<<endl;
NumberOfNode.BFSAlgorithm(2);
return 0;
}

Time & Space Complexity
Complexity of BFS is depend upon the representation of Graph,means how a graph is implemented. For Example :
- if graph is represented by Adjacency List then complexity will be different.
- if graph is represented by Adjacency matrix ,in this case complexity will be different.
- Time Complexity in the case of Adjacency List will be O(|E|+|V|),
where E=Number of Edges. V=Number of Vertices/Nodes, and
Order of O(|E|) can be in range O(1) to O(V^{2}) - Time Complexity in the case of Adjacency Matrix will be O(V^{2}),
- where V=Number of Vertices/Nodes
- Worst Case Space Complexity is O(|V|)
Application of BFS
Breadth-first search can be used to solve many problems in graph theory, for example:
- Use to Find all connected components in a graph.
- Use to Find the shortest path between two nodes.
- Use to Find all nodes within one connected component.
- Used in Garbage_collection and in cheney’s Algorithm.
- Testing a graph for bipartiteness of graph.