Bubble Sort

Bubble Sort is also called sinking sort.This sorting technique is totally based upon the Pass and Iteration.
In every Iteration ,we compare the two elements and swap them if required.
In every Pass one element will be placed their correct position.

Explanation of Bubble Sort By Example

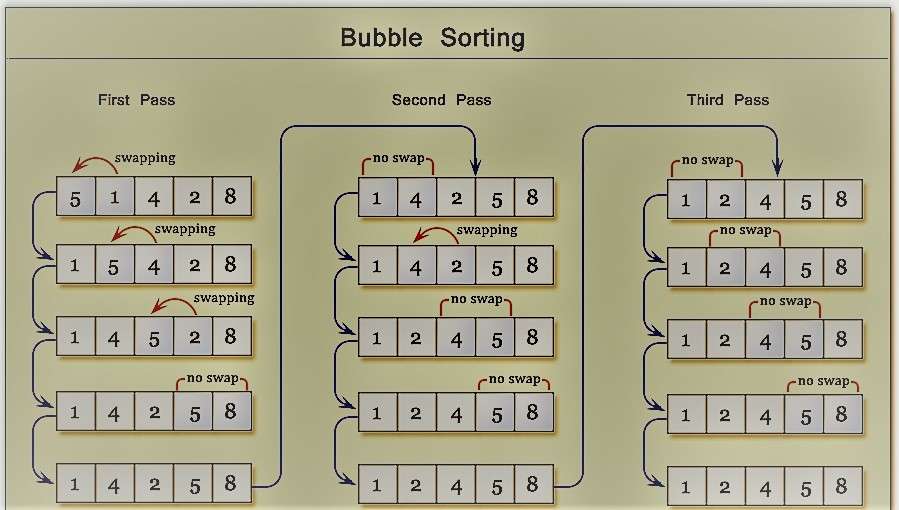
In Bubble Sort,following points must be clear :
1 : Maximum Number of Pass will be always equal to the (n-1), where n=Length of Array.
2 : And In every Pass ,there will be (m-1) Iteration ,where m=Number of Pass.
3 : In every Pass , One element will be place at right position.

Animation of Bubble Sort

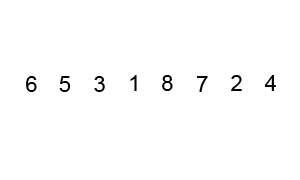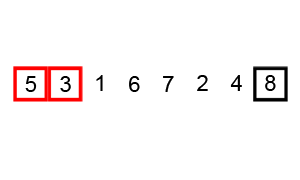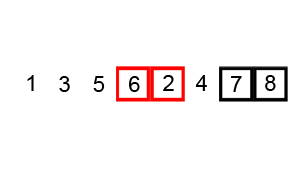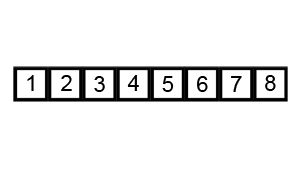
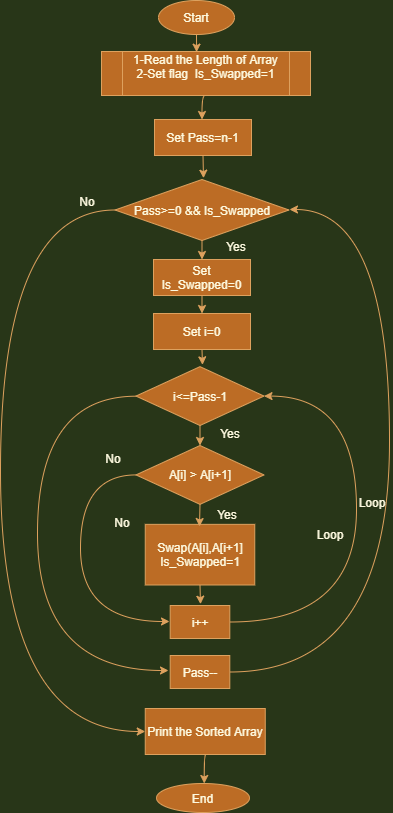
Flow Chart of Bubble Sort

This Flow Chart is based on Code implementation-2,because Code implementation-2 is a good approach to implement the Bubble Sort.

Code Implementation-1

#include <stdio.h>
int main()
{
    int A[]={10,12,5,3,6,7,8};
    int n=sizeof(A)/sizeof(A[0]);
    //Start the Bubble Sort Logic
    for(int Pass=n-1;Pass>=0;Pass--)
    {
        for(int i=0;i<=Pass-1;i++)
        {
            if(A[i]>A[i+1])
            {
                int temp=A[i];
                A[i]=A[i+1];
                A[i+1]=temp;
            }
        }
    }
    //End the Bubble Sort Logic
    for(int i=0;i<n;i++)
    {
        printf("%d\n",A[i]);
    }
    return 0;
}

This Code Implementation is not a good approach,because in Worst,Average and Base case Time Complexity will be O( $n^{2}$ ).

We can improve that implementation by adding one flag variable Is_Swapped,This Variable indicate that whether the array is sorted or not.
If Array is already sorted, So there is no need to go for further Pass.

Code Implementation-2

#include <stdio.h>
int main()
{
    int A[]={4,5,2,1,6,9,7,4};
    int Is_Swapped=1;
    int n=sizeof(A)/sizeof(A[0]);
    //Start the Bubble Sort Logic
    for(int Pass=n-1;Pass>=0 && Is_Swapped;Pass--)
    {
        Is_Swapped=0;
        for(int i=0;i<=Pass-1;i++)
        {
            if(A[i]>A[i+1])
            {
                int temp=A[i];
                A[i]=A[i+1];
                A[i+1]=temp;
                Is_Swapped=1;
            }
        }
    }
    //End the Bubble Sort Logic
    for(int i=0;i<n;i++)
    {
        printf("%d\n",A[i]);
    }
    return 0;
}

In this implementation , we are not performing any Unnecessary Pass,which is not required,because array is already sorted.
Here we are using one flag Is_Swapped ,if there is no swap is required means array is already sorted,then Is_Swapped =0, and Outer Loop will not go for further Pass.
So,In Worst and Average Case Time Complexity will be O( $n^{2}$ ), and In Best Case Time Complexity will be O(n).

Time & Space Complexity

Worst Case Complexity : O( $n^{2}$ )
Best Case Complexity : O(n).
Average Case Complexity : O( $n^{2}$ ).
Space Complexity : O(1).