Merge Sort

• Merge Sort is an general-purpose sorting algorithm which is based on comparison type algorithm.
• Merge Sort is the process of joining/merging two or more sorted files and finally make single bigger sorted file.
• Merge Sort follow the Divide & Conquer design strategy(Will Discussed in details).
• In Merge sort ,we divide the whole array or list until we can not divide further.and then start merging the divided part of array or list in sorted order.
• Merge Sort is the complement of Quick Sort.
• Merge Sort start the process of merging with small files and complete with largest one.
• During the execution,merge sort don’t need extra space,So merge sort is an stable and in-place type algorithm.
• Merge sort can also be applicable whose data structure which are not supporting random searching like linked list etc.

Explanation of Merge Sort by Example

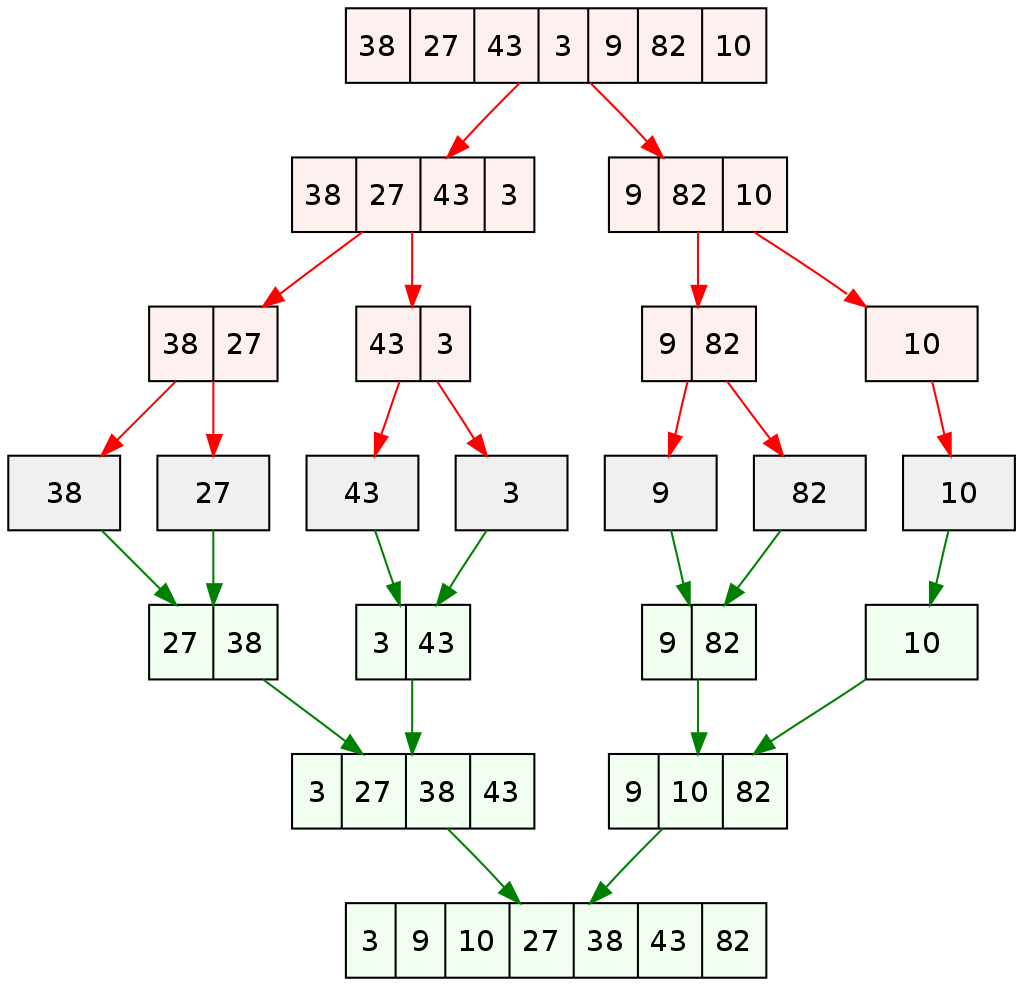
In above figure : Red Color arrow indicates the dividing the whole list and Green Color arrow indicates the conquering or merging the array in sorted order.

Animation of Merge Sort

Code Implementation

#include <stdio.h> 
#include <stdlib.h> 
void merge(int A[], int Low, int mid, int Right) 
{ 
    int i, j, k; 
    int LeftPos = mid - Low + 1; 
    int RightPos = Right - mid; 
  
    //Create a temporary array to handle right and left divided array
    int LeftTemp[LeftPos], RightTemp[LeftPos]; 
  
    /* Copy data to temp arrays LeftTemp[LeftPos], RightTemp[LeftPos] */
    for (i = 0; i < LeftPos; i++) 
         LeftTemp[i] = A[Low + i]; 
    for (j = 0; j < RightPos; j++) 
          RightTemp[j] = A[mid + 1 + j]; 
  
    /* Merge the temp arrays again into A[low..Right]*/
    i = 0; // Starting index of first subarray 
    j = 0; // Starting index of second subarray 
    k = Low; // Starting index of merged subarray 
    while (i < LeftPos && j < RightPos) { 
        if (LeftTemp[i] <= RightTemp[j]) { 
            A[k] = LeftTemp[i]; 
            i++; 
        } 
        else { 
            A[k] = RightTemp[j]; 
            j++; 
        } 
        k++; 
    } 
  
    /* Copy the remaining elements of LeftTemp[]*/
    while (i < LeftPos) { 
        A[k] = LeftTemp[i]; 
        i++; 
        k++; 
    } 
  
    /* Copy the remaining elements of RightTemp[]*/
    while (j < RightPos) { 
        A[k] = RightTemp[j]; 
        j++; 
        k++; 
    } 
} 
void mergeSort(int A[], int Low, int Right) 
{ 
    if (Low < Right) 
    { 
        // Find mid for divide
         //Use this formula for Avoiding Overflow for large Low and Right
        int mid = Low + (Right - Low) / 2; 
  
        // Sort first and second Divided Parts of array 
        mergeSort(A, Low, mid); 
        mergeSort(A, mid + 1, Right); 
        // Merge the divided array
        merge(A, Low, mid, Right); 
    } 
} 

int main() 
{ 
    int A[] = { 7,2,1,4,6,9,5}; 
    int LengthOfArray = sizeof(A) / sizeof(A[0]);
    int Low=0,Right=LengthOfArray-1;
    mergeSort(A, Low,Right); //mergeSort Algorithm
    printf("\nSorted array is \n"); 
    for (int i = 0; i < LengthOfArray; i++) 
    {
        printf("%d ", A[i]); 
    }
    return 0; 
} 

Time & Space Complexity

In Merge Sort,input list is recursively divided into two parts(Sub-problems) and also solved or sort in any order recursively.after Solving the Sub-problems,these are merged, and process will go next sub-problems.
if list or array length is n,then

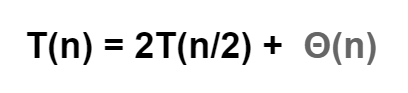
If we apply Master Theorem then Time Complexity will be O(nlogn)

• In merge sort , all the statement will execute completely,thats why in all cases(Best,Worst,Average) complexity will be same,Means
• Worst Case Complexity : O(nlogn)
  Best Case Complexity : O(nlogn)
  Average Case Complexity : O(nlogn)
• Space Complexity : O(n) {In worst case}

Important Notes

• When we need guaranteed complexities then merge sort is best choice because of their stability in all cases.
• Merge Sort is faster and more efficient as compare to Quick Sort when data list are large. but its not a good choice for small data list.