- Quick Sort is an comparison based sorting algorithm.
- It is also called partition exchange sort.
- Quick sort is based on the Divide & Conquer design strategy.
- Quick Sort is an complement of Merge Sort.
- Quick Sort is a good choice when Data List is small.
Working Process of Quick Sort
Here pivot element can be any element, but generally we choose following types of element as a pivot :
- Pick first element as pivot(Preferable)
- Pick last element as pivot.
- Pick a random element as pivot.
- Pick median as pivot.
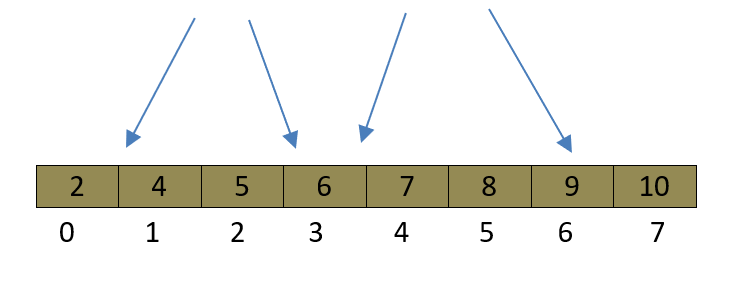
Step-1 : Suppose an array X[] ={6,2,5,7,8,9,4,10} .
Step-2 : choose left most element of array as a pivot.pivot element is pivotValue=6.
Step-3 : scan from left to right , and from left, choose an element which is just greater than pivotValue, which is 7 (pivotValue < 7),Now, find the index of 7, that is i=3.
Step-4 : scan from right to left and from right, choose an element which is just less than or equal to the pivotValue , which is 4 (pivotValue >= 4), Now find the index of 4 , that is j=6.
Step-5 : option-1 : if i<j then swap(X[i] ,X[j}). and repeat the Step(2,3,4) again.
option-2 : if i>=j then swap(X[j],pivotValue) . and Now in this situation pivotValue will divide the whole array into two part ,left part will be always less than pivotValue, right part will be always greater than pivotValue and pivotValue is an Sorted Position,left and right part are not sorted ,we will again repeat Step(2,3,4,5) for left and right part.
Explanation of Quick Sort by Example
- Quick Sort use pivot value to divide the array(Generally left most element we choose as a pivot) into two parts,this is called partitioning.
- left part will be always less than pivot, and right part will be always greater than pivot.
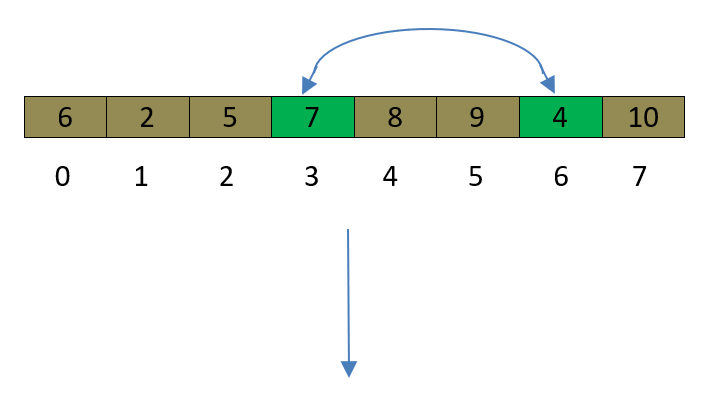
- pivotValue=6.
- pivotValue < 7,now i=3.
- pivotValue >4,now j=6.
- i<j ,swap (7,4)
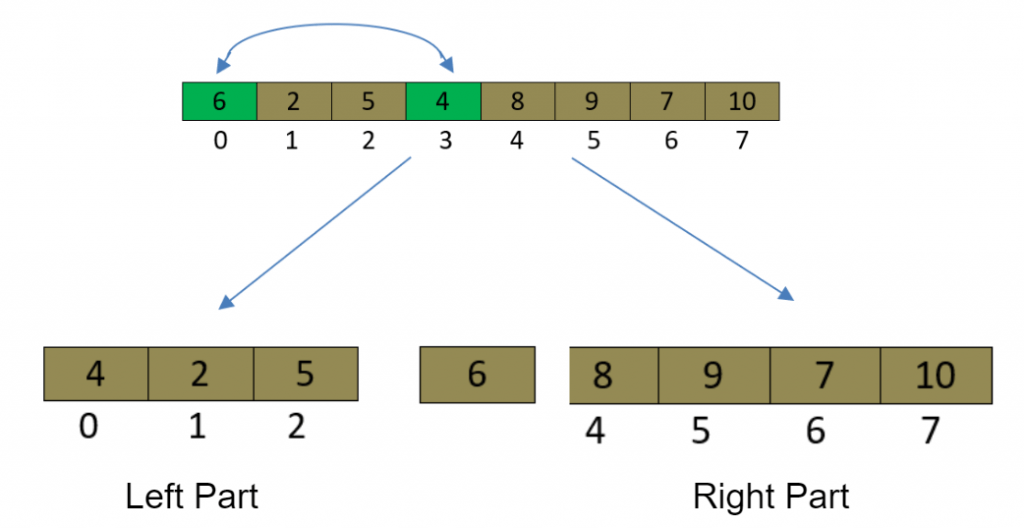
- pivotValue=6.
- pivotValue < 8,now i=4
- pivotValie > 4,now j=3.
- i>=j,swap(pivotValue,4)In this situations Array will be divid into two following parts.
Now we will take Left Part and Right Part separately,and solve it.
Left Part
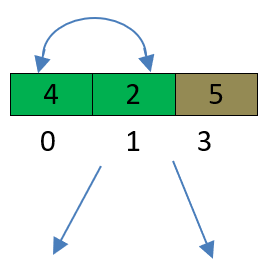
- pivotValue=4.
- pivotValue < 5,now i=3.
- pivotValue>2,now j=1.
- i>=j,swap(pivotValue,2),In this situations Array will be divid into two following parts.
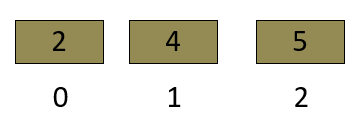
- Now Left Part has been sorted.
- We will join/conquer with the Right Part.
Right Part
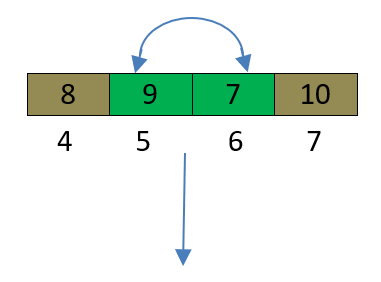
- pivotValue=8.
- pivotValue <9,now i=5.
- pivotValue >7,now j=6.
- i<j,swap(9,7).
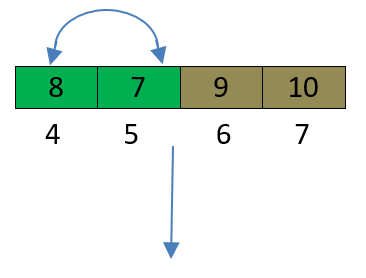
- pivotValue=8.
- pivotValue <9, now i=6.
- pivotValue >7,then j=5.
- i>=j,swap(pivotValue,7),In this situations Array will be divid into two following parts.
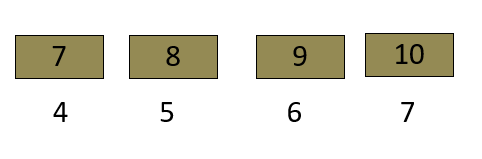
- Now Right Part has been sorted.
- We will join/conquer with the Left Part.
Now every element has been placed their correct position.So we will merge them.
Animation of Quick Sort
Code Implementation
#include <stdio.h>
#include <iostream>
using namespace std;
// for swapping an elements
void swap(int* SmallerElement, int* HigherElement)
{
int temp = *SmallerElement;
*SmallerElement = *HigherElement;
*HigherElement = temp;
}
int partition (int A[], int Low, int High)
{
int pivotValue = A[High]; //Choose pivotValue
int smallerElementIndex = (Low - 1); // smaller element index
for (int i = Low; i <= High - 1; i++)
{
// If current element is smaller than the pivot
if (A[i] < pivotValue)
{
smallerElementIndex++; // increment index of smaller element
swap(&A[smallerElementIndex], &A[i]);
}
}
swap(&A[smallerElementIndex + 1], &A[High]);
return (smallerElementIndex + 1);
}
void quickSort(int A[], int Low, int High)
{
if (Low < High)
{
int partitionedIndex = partition(A, Low, High);
quickSort(A, Low, partitionedIndex - 1);
quickSort(A, partitionedIndex + 1, High);
}
}
int main()
{
int A[] = {6,2,5,7,8,9,4,10} ;
int LenghtOfArray = sizeof(A) / sizeof(A[0]);
quickSort(A, 0, LenghtOfArray - 1);
printf( "Sorted array is : \n") ;
for (int i = 0; i < LenghtOfArray; i++)
printf("%d\t",A[i]);
return 0;
} 
Time & Space Complexity
As per above code implementation,we can write recurrence relation for quick sort is follows :
T(n) = T(k) + T(n-k-1) +(n) where k=elements ,which are smaller than pivot value.
- Worst Case : When pivot is smallest or greatest element for all the partition calling ,then in this situation , k=0, because there is not element which is less than pivot.Worst case occurs when array is already sorted in decreasing order and we chose first element as a pivot. So Recurrence relation will be in worst case :
T(n) = T(0) + T(n-0-1) +(n) T(n) = T(n-1) +
(n) If we apply Subtraction and Conquer master theorem,then T(n) =O(n^{2})
- Best Case : When Each partition calling divides the array into two parts then Recurrence relation will be in best case :
T(n) = 2T(n/2) +(n) If we Apply master theorem then T(n)=O(nlogn)
- Average Case : When division of array is unknown,means we don’t know where the splits happens. So we will consider the complexities of all possible permutations and take the average of all complexities,but its not an easy task to find all possibilities,So directly we are taking an average case :
T(n) = T(n/9) + T(9n/10) +(n) If we apply Subtraction and Conquer master theorem,then T(n)=O(nlogn)
- Worst case space Complexity: O(1)
Important Notes
- Quick Sort performance is totally depend upon the pivot,So we have to choose pivot very carefully.
- Good idea for choosing an pivot is : take any three element of array and calculate the median of them,this median will be best choice as a pivot.
- if we choose pivot randomly ,then Quick Sort is called Randomized Quick Sort.
- General implementation of Quick Sort is not stable, but we know that sorting algorithm can be convert into Stable type algorithm.
- Quick Sort qualify comes under the In-place type algorithm in broad definition,because in Quick Sort implementation we use some extra space only in recursive call.