Note : To understand Topological Sort ,we recommend you,please first refer Graph Data Structure and Graph Algorithm Section.
- Topological Sorting of a Directed Graph is a linear sorting of its nodes/vertices.For example Directed Edge UV means U is pointing to V and not Vice Versa ,means you have to visit on U first then V ,means if you want visit on V then you have to first visit on U.
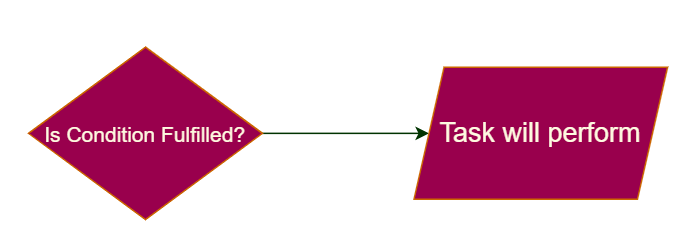
- Topological Sorting based on the Conditional Processing,means when condition is fulfilled then processing will occurs.
Example :In Below diagram ,When Condition is true then will go for Task Processing.
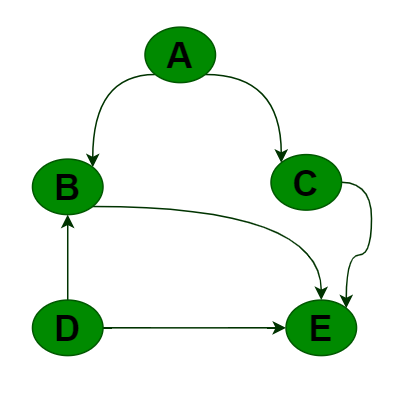
- for Directed edge AB, B should never appear before A.
- for Directed edge ABCE, A always appear before B ,C and E. and B always appear before E,and C always appear before E.
- Directed edge DE, D always appear before E.
- Topological Sorting is only applicable for Directed Graph .For Undirected Graph Topological sorting is impossible.
- For Topological Sorting ,Our Graph must be free from the Cycle.
means Graph should be Acyclic. - Graph must be DAG type means DAG(Directed Acyclic Graph).
- Topological Sorting produce linear ordering output of vertices.
- Broadly we can say that Topological Sorting is based on Depth First Search(DFS).
- For every DAG, atleast one topological sort is possible.
Working Process of Topological Sort
We have to follow the below step to sort the graph. Suppose a Graph G(V,E) where V ={Set of Vertices} , E={Set of Edges}.We use two Data Structure , Stack and Queue(Q). Stack(S) use for Sorting sequences of Vertices or Sequence of visited Vertices. Queue is used to store the vertices which have In-degree 0.
- Step-1 : Compute the In-degree of all vertices and insert into Queue Q, which vertices have In-degree 0.
- Step-2 : remove one vertex from the Queue and push into Stack S.
- Step-3 : Find out the In-degree of all vertices and if any vertex have 0 In-degree then insert those vertices into Queue Q.
- Step-4 : Repeat Until Queue become empty.
Explanation of Topological Sort by Example
Below is the Graph G(V,E). initialized one queue Q which is empty and also one Stack S ,which is also empty :
- Green Color nodes means visited node.
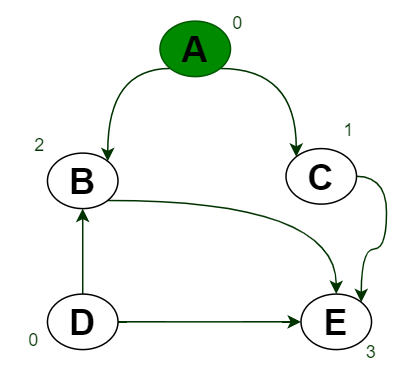
- Here Only Vertices A and D have In-degree 0.
- So insert A and D into Queue Q So Q={A,D}
- Remove A from Queue and push into Stack S,
So S={A}. - Mark A as visited means color it by Green.
- Find the again In-degree of All Vertices.
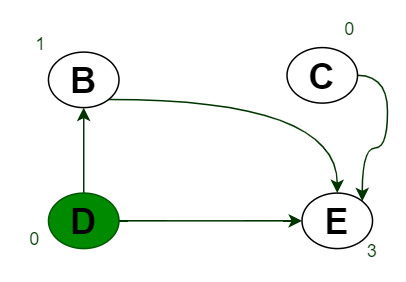
- Queue is Q={D}.
- here only D and C have In-degree 0.
- Insert C into Queue Q and D is already present in Q ,So need to insert.
Queue Q={D,C}. - Remove D from Queue and push into Stack S,
- So S={A,D}.
- Mark D as visited means color it by Green.
- Find the again In-degree of All Vertices.
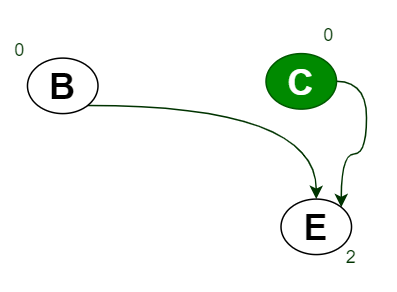
- Queue is Q={C}.
- here only B and C have In-degree 0.
- Insert B into Queue Q and C is already present in Q ,So need to insert.
Queue Q={C,B}. - Remove C from Queue and push into Stack S,
- So S={A,D,C}.
- Mark C as visited means color it by Green.
- Find the again In-degree of All Vertices.
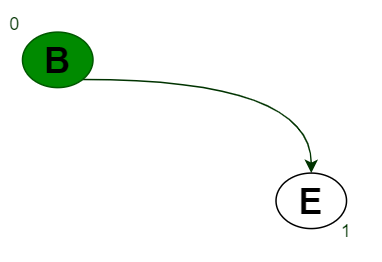
- Queue is Q={B}.
- here only B has In-degree 0.
- B is already present in Q ,So need to insert.
Queue Q={B}. - Remove B from Queue and push into Stack S,
- So S={A,D,C,B}.
- Mark B as visited means color it by Green.
- Find the again In-degree of All Vertices.

- Queue is Q={}.
- Now Queue Q is empty
So Vertex E will push into Stack S. So S={A,D,C,B,E}.
So Topological Sort Sequence will be the Stack S{A,D,C,B,E}.means Sorting sequence is ADCBE.
There can be more than one topological sort sequences like ACDBE is also correct.
Animation of Topological Sort
Code Implementation
#include<stdio.h>
#include<stack>
#include<iostream>
#define VERTICES 5
using namespace std;
stack<int> stk; // Create one integer stack
// Graph is represented by Adjacency Matrix.
int CreateGraph[VERTICES][VERTICES] = {
{0, 1, 1, 0, 0},
{0, 0, 0, 0, 1},
{0, 0, 0, 1, 1},
{0, 1, 0, 0, 1},
{0, 0, 0, 0, 0}
};
void topologicalSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<VERTICES; v++) {
if(CreateGraph[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topologicalSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void ApplyTopologicalSort() {
bool Isvisited[VERTICES]; // Create one boolean type array of size VERTICES.
for(int i = 0; i<VERTICES; i++) // Makes all Vertices are Un-visited.
Isvisited[i] = false;
for(int i = 0; i<VERTICES; i++) //Perform topological sort for Un-visited Node.
if(!Isvisited[i])
topologicalSort(i, Isvisited, stk);
}
main() {
ApplyTopologicalSort();
printf("topological Order Sequence :");
while(!stk.empty()) {
switch(stk.top())
{
case 0:
cout << "A" << " ";
break;
case 1:
cout << "B" << " ";
break;
case 2:
cout << "C" << " ";
break;
case 3:
cout << "D" << " ";
break;
case 4:
cout << "E" << " ";
break;
case 5:
cout << "F" << " ";
break;
}
stk.pop();
}
}
Time & Space Complexity
Complexity of Topological Sort is depend upon the representation of Graph,means how a graph is implemented. For Example :
- if graph is represented by Adjacency List then complexity will be different.
- if graph is represented by Adjacency matrix ,in this case complexity will be different.
- Time Complexity in the case of Adjacency List will be O(|E|+|V|),
- where E=Number of Edges. V=Number of Vertices/Nodes, and
- Order of O(|E|) can be in range O(1) to O(V^{2})
- Time Complexity in the case of Adjacency Matrix will be O(V^{2}),
- where V=Number of Vertices/Nodes
- Worst Case Space Complexity is O(|V|)
Application
- Can be use to representing course prerequisites
- Evaluation of formulae in spreadsheet.
- Detecting deadlocks Points
- Can be use in Pipeline of computing jobs
- Can be use to Checking for symbolic link loop
IxwyfCqaeAKptnE