Traversal is a process to visit on every node at least once.Traversal process already discussed in Linked list ,Queue,Stack data structure where Traversing was sequential order.but in Binary tree we can traverse the all node by different different ways.for traversal, we have to start from root node always,we can not access the node randomly.
1-Types of Traversing :
There are four types of traversing method :
Here D means Visiting the current node, L means visiting the left child of current node, R means visiting the right child of current node.
- Preorder traversal (DLR)
- Inorder traversal(LDR)
- Postorder traversal(LRD)
- Level Order traversal.
1.1-Preorder Traversal
In preorder traversal, first we have to visit the root node,then visit the left subtree and right subtree.
Process is defined as follows :
- Visit the root node.
- process the left subtree
- process the right subtree.
1.1.1-Working Process of Preorder Traversal
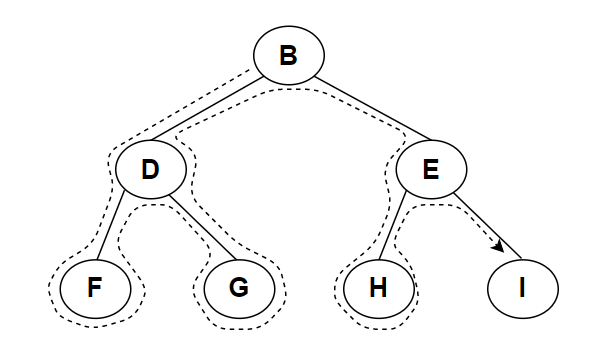
- B is the root node.
- Left subtree of B is DFG.
- for subtree DFG, Preorder sequence will be DFG.
- Right subtree of B is EHI.
- for subtree EHI,Preorder sequence will be EHI.
- Preorder Traversal order of tree is BDFGEHI.
1.1.2-Code Implementation of Preorder Traversal
Preorder traversing can be implement in two ways :
1- Recursive Implementation
2- Non-Recursive Implementation.
- Debug the recursive and Non-recursive code with the below Binary tree :
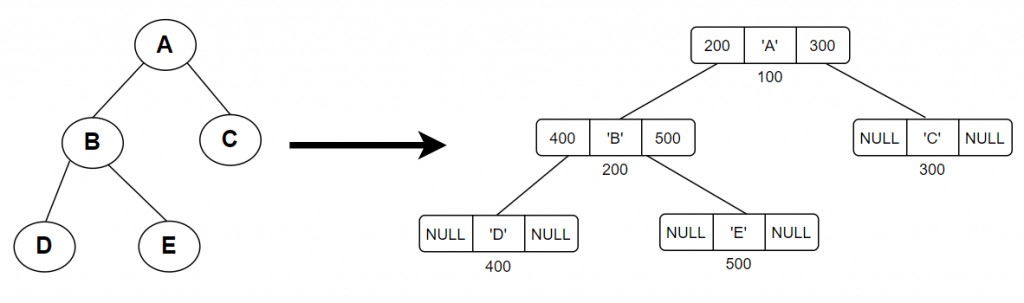
1.1.2.1- Recursive Implementation of Preorder Traversal
#include <stdio.h>
#include <iostream>
#include<conio.h>
#include<math.h>
#include<stdlib.h>
struct BinaryTreeNode // Node Structure Initialization
{
char data; // for data element
struct BinaryTreeNode* left; //for storing the address of left child
struct BinaryTreeNode* right; // for storing the address of right child
};
// PreOrder Traversing method.
void PreOrderTraversing(struct BinaryTreeNode* rootNode)
{
if (rootNode)
{
std::cout << rootNode->data << " ";
PreOrderTraversing(rootNode->left);
PreOrderTraversing(rootNode->right);
}
}
int main()
{
//initialize 5 node to create the binary tree.
struct BinaryTreeNode* A = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* B = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* C = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* D = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* E = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
//address arrangement.
A->left = B;
A->right = C;
B->left = D;
B->right = E;
//leaf node has zero child.
C->left = NULL;
C->right = NULL;
D->left = NULL;
D->right = NULL;
E->left = NULL;
E->right = NULL;
//Data Initilization.
A->data = 'A';
B->data = 'B';
C->data = 'C';
D->data = 'D';
E->data = 'E';
// call the function to print the Preorder Sequence
printf("PreOrder Traversal will be : ");
PreOrderTraversing(A);
_getch();
return 0;
}
1.1.2.2- Non-Recursive Implementation of Preorder Traversal
#include <stdio.h>
#include <iostream>
#include<conio.h>
#include<math.h>
#include<stdlib.h>
#include<stack>
struct BinaryTreeNode // Node Structure Initialization
{
char data; // for data element
struct BinaryTreeNode* left; //for storing the address of left child
struct BinaryTreeNode* right; // for storing the address of right child
};
// PreOrder Traversing method.
void PreOrderTraversing(struct BinaryTreeNode* rootNode)
{
//For Stack ,we used stack library of STL.
std::stack <struct BinaryTreeNode*> StackForRoot;
while (true)
{
while (rootNode)
{
std::cout << rootNode->data << " ";
//store the rootNode of all node into the stack.
StackForRoot.push(rootNode);
rootNode = rootNode->left;
}
//When there is no left node then pop the stack
if (!StackForRoot.empty())
{
//Store the top value of stack.
rootNode=StackForRoot.top();
//Pop the top value.
StackForRoot.pop();
rootNode = rootNode->right;
}
else
break;
}
}
int main()
{
//initialize 5 node to create the binary tree.
struct BinaryTreeNode* A = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* B = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* C = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* D = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* E = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
//address arrangement.
A->left = B;
A->right = C;
B->left = D;
B->right = E;
//leaf node has zero child.
C->left = NULL;
C->right = NULL;
D->left = NULL;
D->right = NULL;
E->left = NULL;
E->right = NULL;
//Data Initilization.
A->data = 'A';
B->data = 'B';
C->data = 'C';
D->data = 'D';
E->data = 'E';
// call the function to print the Preorder Sequence
printf("PreOrder Traversal will be : ");
PreOrderTraversing(A);
_getch();
return 0;
}
1.1.3- Time & Space Complexity of PreOrder Traversal
- For Recursive Implementation : Time Complexity will be O(n),
and Space Complexity will be O(n). - For Non-Recursive Implementation : Time Complexity will be O(n),and Space Complexity will be O(n).