An AVL tree is a self-balancing binary search tree where the balance factor of every node is kept within a specific range to ensure that the tree remains balanced.
In an AVL tree, the balance factor of every node must be in the range [-1, 0, 1]. If, at any point during insertion or deletion, the balance factor of a node violates this range, the tree is considered unbalanced, and rotations are performed to restore balance.
Let’s consider the four possible AVL tree violations and understand them with examples:
- when an insertion into the left subtree of the left child of node —-apply—–> LL rotation
- when an insertion into the right subtree of the left child of node. —-apply—–> LR rotation
- when an insertion into the right subtree of right child of node. —-apply—–> RR rotation
- when an insertion into the left subtree of right child of node. —-apply—–> RL rotation
Above is the main reason of violations. So as per the violations we are applying some rotations on the node to get back the self balanced binary tree.
The LL and RR are single rotations and LR and RL are double rotations. For a tree to be unbalanced, minimum height must be at least 2, Let us understand each rotation
Rotations:
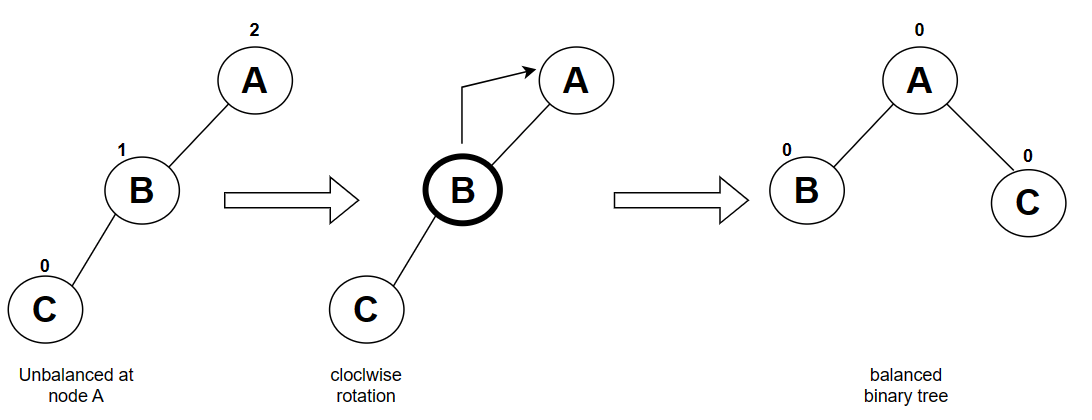
1-LL rotation :
The binary search tree (BST) lost the balance because a node C is added as a left child of the B, and balance factor of A became 2 , so it’s not coming under [-1,0,1] then we have to execute a left-left (LL) rotation. LL rotation is a clockwise rotation, is employed on the edge below a node with a balance factor of 2.
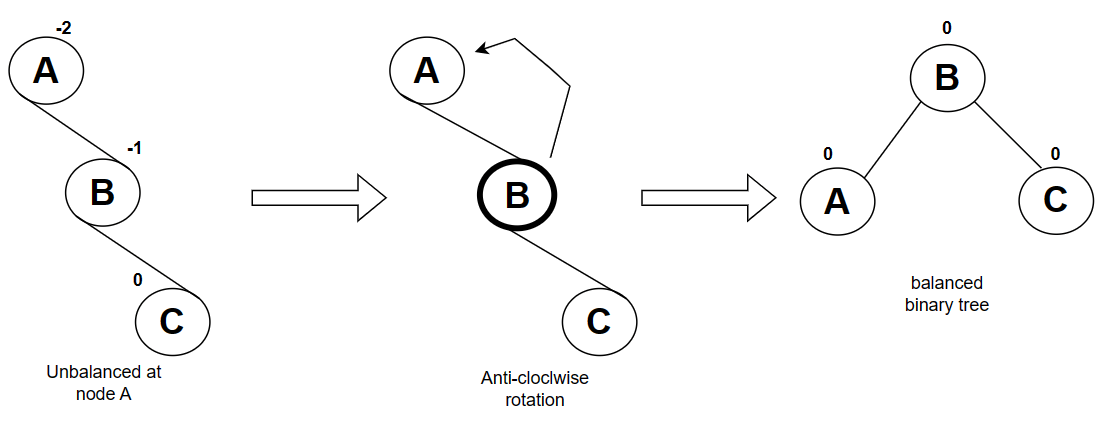
2-RR rotation :
The binary search tree (BST) lost the balance because a node C is added as a right child of the B, and balance factor of A became -2 , so it’s not coming under [-1,0,1] then we have to execute a right-right (RR) rotation. RR rotation is a Anti-clockwise rotation, is employed on the edge below a node with a balance factor of 2.
3-LR rotation :
Performing double rotations poses a greater challenge compared to single rotations. The LR rotation is essentially equivalent to the sum of RR rotation and LL rotation. In other words, the initial step involves conducting an RR rotation on a subtree, followed by an LL rotation on the entire tree. When we refer to the “full tree,” we are pointing to the initial node along the path of the inserted node. This node should have a balance factor different from -1, 0, or 1.
Example:
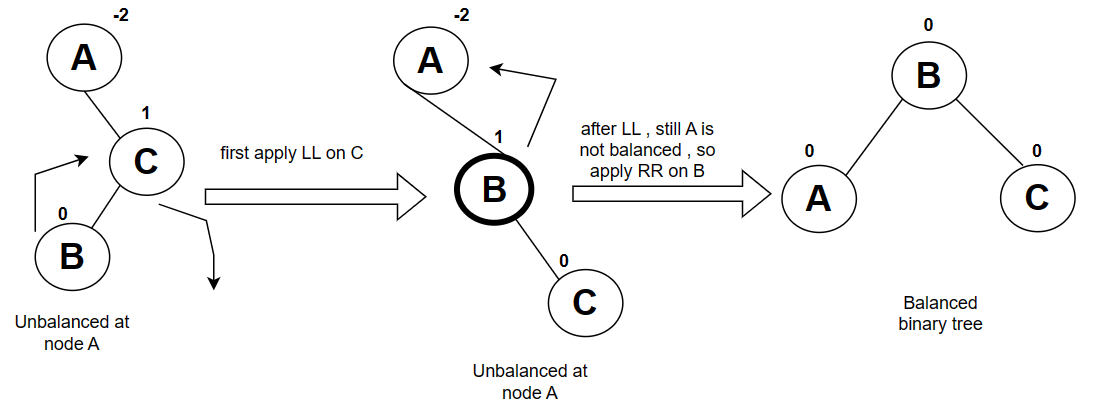
B is inserted to the left of C and right of A , because of this insertion C has become unbalanced. and here node is inserted right node of the left subtree , so LR rotation is required.
LR rotation = RR + LL rotation
4-RL rotation :
As already discussed that, Performing double rotations poses a greater challenge compared to single rotations. The RL rotation is essentially equivalent to the sum of LL rotation and RR rotation. In other words, the initial step involves conducting an LL rotation on a subtree, followed by an RR rotation on the entire tree. When we refer to the “full tree,” we are pointing to the initial node along the path of the inserted node. This node should have a balance factor different from -1, 0, or 1.
Example:
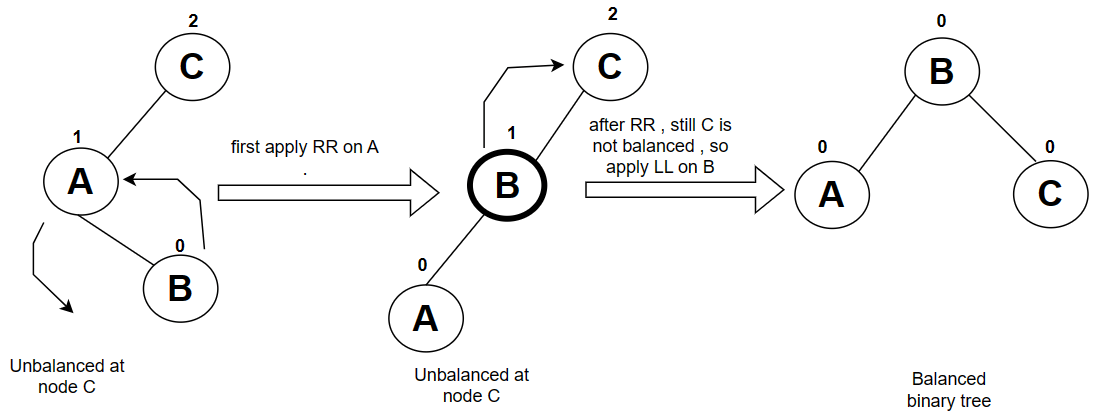
B is inserted to the right of C and left of A , because of this insertion A has become unbalanced. and here node is inserted left node of the tight subtree , so RL rotation is required.
RL rotation = LL + RR rotation